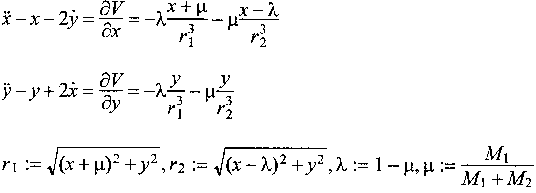
von Dr. Werner Eberl
2.1 Das eingeschränkte Dreikörperproblem
2.2 Nichtlineare Differentialgleichung des Dreikörperproblems
3.1 Berechnung nach Bremer Methode
3.2 Berechnung nach Karlsruher Methode
5.1 Anwendung der Ergebnisse auf unser Sonnensystem
Mit der Berechnung von Planetenbahnen beschäftigten sich Wissenschaftler schon in der Antike. Nach dem Aufkommen der Chaostheorie bekam dieses Thema einen neuen Aspekt. Vor allem eine Frage beschäftigte die Wissenschaftler: Verhalten sich Planetenbahnen chaotisch? In dieser Arbeit wird auf die Berechnung von Planetenbahnen nach H.-O. Peitgen und P. H. Richter [3] an der Universität Bremen (1986) und nach E. Adams [1] am Institut für angewandte Mathematik in Karlsruhe eingegangen. Beide Teams von Wissenschaftlern bezogen sich bei ihren Berechnungen auf das eingeschränkte Drei-Körper-Problem (2.1). Peitgen und Richter erhielten als Ergebnis eine Bahn, die sie als chaotisch bezeichneten. Adams und sein Team kamen auf eine periodische Bahnkurve. Da Peitgen und Richter die Daten, die ihrer Berechnung zugrunde lagen, erst am 1.11.1993 bekanntgaben, war es E. Adams erst dann möglich die Bahn unter Anwendung von Einschließungs-Methoden zu berechnen, was im wesentlichen eine Bestätigung der Kurve von Peitgen und Richter ergab [1]. 1992 ist es Z. Xia in Melnikov Method and Transversal Homoclinic Points in the Restricted Three-Body Problem gelungen, den mathematischen Existenzbeweis für das Auftreten von Chaos beim eingeschränkten Drei-Körper-Problem zu führen. Im letzten Teil dieser Arbeit sollen daraus resultierende mögliche Konsequenzen auf das Sonnensystem diskutiert werden.
Alle Berechnungen, die in dieser Arbeit besprochen werden, beziehen sich auf das eingeschränkte Drei-Körper-Problem (3KP). Im 3KP bewegt sich ein kleiner Planet mit der Masse m im Schwerefeld zweier Sterne mit den Massen M1 und M2. Dabei gilt: M1 >> m und M2 >> m. Die beiden großen Körper bewegen sich gleichförmig auf einer gemeinsamen Kreisbahn (Bild 1). Beim eingeschränkten 3KP wird nur der Einfluß der beiden großen Massen auf die kleine Masse m berücksichtigt, wohingegen im allgemeinen 3KP auch der Einfluß der kleinen Masse m auf die Bewegungen der großen Körper und deren gegenseitige Störungen beinhaltet sind. Zur besseren Interpretation der berechneten Bahnkurven des kleinen Körpers beziehen sich die Darstellungen (Bild 2/3/4) auf eine an den großen Massen befestigte rotierende Basis in der Ebene der Hauptmassen, das heißt man erhält ein "stehendes" Bild in bezug auf M1 und M2.

Das eingeschränkte 3KP führt zu einer nichtlinearen Differentialgleichung der folgenden Form:
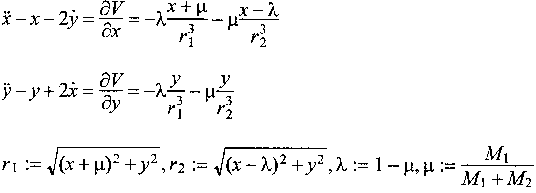
µ ist dabei der Anteil der Masse M1 an der Gesamtmasse (M1+M2). Die Lösungen der obigen Gleichungen repräsentieren Bahnkurven des kleinen Körpers. Nichtlineare Differentialgleichungen können Analytisch nicht gelöst werden. Die Lösung muß mit Hilfe von numerischen Verfahren angenähert werden. Das Problem dabei ist, um die Lösung (im Fall des 3KP die Koordinaten des kleinen Körpers) für einen bestimmten Zeitpunkt zu errechnen, man ausgehend von einem Startwert für sämtliche Zeitpunkte, die vor dem Gesuchten liegen, die jeweiligen Lösungen berechnen muß. Ein sehr verbreitetes Verfahren zur numerischen Integration ist das Runge-Kutta-Verfahren mit fester Integrationsschrittweite. Je kleiner die Integrationsschritte werden, desto mehr Rechenschritte sind notwendig, um den Ort der kleinen Masse m zu einem bestimmten Zeitpunkt zu bestimmen. Es ist folglich ein enormer Rechenaufwand nötig, um langfristige Prognosen über das Verhalten des Systems zu machen. Laut E. Adams [1] können bei einigen mathematischen Verfahren zur Berechnung von nichtlinearen DGL Rundungs- und Diskretisierungsfehler, die im Computer immer gemacht werden, dazu führen, daß die berechnete und die tatsächliche Lösung weit auseinanderläuft.
Die Bremer Rechnung von 1985 benutzt regularisierende Koordinaten, in denen die Singularität, die in der Nähe der Stöße des Testkörpers mit den beiden Hauptmassen auftreten können, vermieden wird [3]. Die Wissenschaftler benutzten folgende Gleichungen, die aus den Gleichungen unter 2.2 durch Transformation auf eine neue Zeit entstanden:

Es wurden folgende Anfangsbedingungen gewählt:
µ = 1/2, d.h. die beiden großen Körper haben gleiche Massen. (x,u) = (-0.14188346, 0) im Poincaréschnitt y = 0, >0 bei der Energie E = -1,75. Als Projektionsebene der Bahn nahmen sie die (x, y)-Ebene. Als Ergebnis erhielten sie die in Bild 2 gezeigte Bahnkurve.
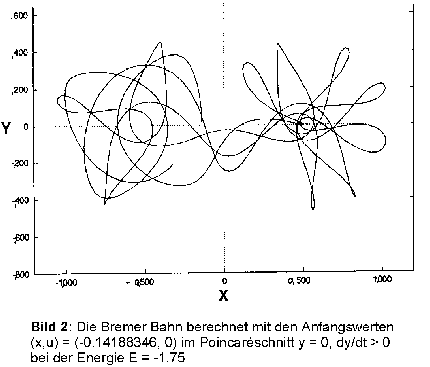
Wie sich unschwer erkennen läßt ist die Bahnkurve im berechneten Zeitintervall nicht periodisch. H.-O. Peitgen und P. Richter sahen darin eine Bestätigung dafür, daß das 3KP chaotisch ist. Sie veröffentlichten darum 1986 die Kurve in [6].
Die Karlsruher Wissenschaftler berechneten die Gleichungen von 2.2 mit Hilfe des Runge-Kutta-Verfahrens mit einer festen Schrittweite von h = 10E-3. Sie benutzten die Anfangsbedingungen: (x, y, vx, vy) = (1.2, 0, 0, -1.04935750983), µ = 1/82.45 (charakterisiert das System Erde-Mond). Sie konnten nicht die gleichen Anfangswerte wie die Bremer Wissenschaftler benutzen, da sich diese ihre Startwerte nicht notiert hatten und diese erst sehr viel später (1993) rekonstruieren und bekanntgeben konnten. Die Berechnung lieferte die in Bild 3 gezeigte, periodische Bahnkurve. Es läßt sich zeigen, daß durch Veränderung der Schrittweite auf h = 5*10E-3 man die in Bild 4 gezeigte Bahn erhält.
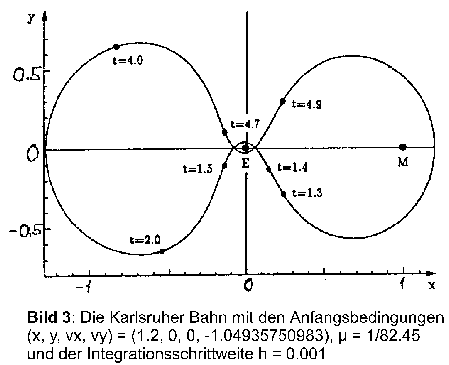
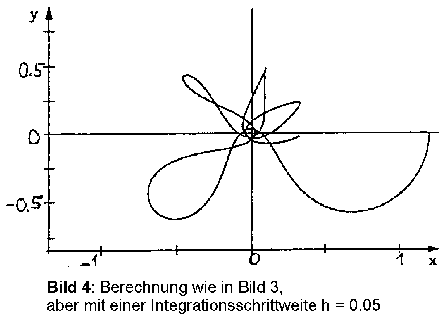
Die Karlsruher schlossen nun aus der Ähnlichkeit der Bahn in Bild 4 und der Bahn der Bremer Rechnung (Bild 2) darauf, daß der chaotische Verlauf durch eine zu kleine Schrittweite bei der Bremer Berechnung entstanden ist. Sie nennen die so entstandenen Unregelmäßigkeiten in [7] "Computational Chaos".
Wie oben gezeigt (Bild 2 u. Bild 3) erhielten beide Teams unterschiedliche Ergebnisse. Diese Tatsache benutzte der Autor Peter Brügge zu einem Artikel im Spiegel [2] in dem er die Bremer Wissenschaftler und den 'Kult mit dem Chaos' stark angriff. Daraufhin entstand zwischen den Wissenschaftlern eine Kontroverse, die auch ein Thema bei der 3. Jahrestagung der Chaosgruppe in München war. Die Bremer Physiker erklärten die unterschiedlichen Ergebnisse folgendermaßen:
Zur Aussage der Karlsruher, sie hätten eine falsche Integrationsschrittweite benutzt, schreiben sie folgendes: "Der Schluß von der Ähnlichkeit zweier Bilder (Bild 2 und Bild 4, der Verf.) auf die Ähnlichkeit der gemachten Fehler ist ein trivialer logischer Fehlschluß".
Tatsächlich stellte sich Ende 1993, als die Anfangsbedingungen der Bremer Bahn bekanntgegeben werden konnten, die Richtigkeit der Bremer Trajektorie heraus. Adams und sein Team konnten, wie in der Einleitung erwähnt, die Bremer Bahn mit Hilfe von total fehlerkompensierten Einschließungs-Methoden [8] bestätigen. Es gelang ihnen allerdings auch zu zeigen, daß das von Peitgen & Richter verwendete numerische Verfahren bei Anwendung auf nichtlineare Probleme mit komplizierten Bahnkurven prinzipiell nicht zuverlässig ist [1]. Außerdem behauptet Adams, aus dem Segment einer Bahnkurve, so wie es in Bild 2 zu sehen ist, könne nicht auf Chaos geschlossen werden, da chaotische Strukturen nur für überabzählbare Mengen von Lösungen auf halbunendlichen Zeitintervallen erklärt seien. Andererseits konnte Z. Xia beweisen, daß Chaos beim 3KP auftreten kann (siehe Einleitung). Daraus folgt, daß die Bremer Bahnkurve chaotisch sein kann, mit endgültiger Sicherheit läßt sich dies aber ohne weiteres nicht sagen.
Da bei dem mit drei beteiligten Massen recht einfachen und überschaubaren Modell des eingeschränkten 3KP, chaotisches Verhalten nachgewiesen werden konnte, ist anzunehmen, daß viel komplexere Systeme, wie etwa unser Sonnensystem auch chaotisches Verhalten zeigen können.
Dies hätte zur Folge, daß sich die Bahnen der Planeten der langfristigen Berechenbarkeit entziehen, weil bei chaotischen, also nichtperiodischen Bahnkurven, jeder noch so kleine Fehler in der Bestimmung der Ausgangsbedingungen multiplikativ zunimmt [4]. Im Gegensatz dazu kann man bei periodisch verlaufenden Bahnen zu jedem beliebigen Zeitpunkt den Ort mit einem gleichbleibenden Fehler berechnen. Der Fehler ist dabei gleich dem Fehler den man bei der Bestimmung der Ausgangsposition macht.
Rechnungen von Jacques Laskar für die Erde deuten darauf hin, daß schon eine Meßungenauigkeit der Erdbahn von 15 Metern nach 100 Millionen Jahren zu einer Ungenauigkeit von 100 Prozent für die Bahnparameter unseres Heimatplaneten führt [4]. Es läßt sich also sagen, daß sich unser Sonnensystem durchaus chaotisch verhalten kann, sich dies aber erst in für uns ungeheuer großen Zeiträumen äußert.
[1] Adams Ernst, Sind chaotische Strukturen in Phasenräumen zuverlässig nachweisbar? Chaos und Strukturbildung, p. 17, München, 1994
[2] Peter Brügge, Ausbreitung und Mißbrauch der Chaostheorie, Der Spiegel, 47, Nr. 40, p. 232, 1993
[3] Holger R. Dullin und Peter H. Richter, Planetenbahnen nach Bremer und Karlsruher Berechnung, Chaos und Strukturbildung, p. 53, München, 1994
[4] Planeten laufen aus dem Ruder, Geoskop, p. 198, Geo, Nr. 5, 1990
[5] James Gleick, Chaos - die Ordnung des Universums, München, 1988
[6] H.-O. Peitgen, P. H. Richter, The Beauty of Fractals, Berlin, Heidelberg, New York: Springer 1986
[7] E. Adams, in Scientific Computing with Automatic Result Verification, eds. E. Adams, U. Kulisch, pp. 423-526. Boston: academic Press 1992
[8] R. Lohner, Einschließung der Lösung gewöhnlicher Anfangs- und Randwertaufgaben und Anwendungen, Dissertation, Karlsruhe, 1988
Martin Krause,
krause@bv.rz.fh-muenchen.de, Aubachstr. 10, 82229
Seefeld